思考・考察
Learning about genetic programming
Tang
Preface
Edward mentioned he generate impulse responses (IRs) for convolution reverberation using a classical Genetic Algorithm (GA) when he was a master’s student. We may be able to apply similar techniques to other LTI or non-LTI systems.
For me, one of the most interesting topics in the presentation is the different types of Genetic Algorithms.
Background
“Natural selection, survival of the fittest”, Darwin put forward the famous theory of biological evolution, that is, all animals and plants evolved from earlier, more primitive forms. Genetic programming applies this evolutionary process in the fields of mathematics and computer science: from the primitive and rough program population with a relatively large base, the paternal line is selected by evaluating the fitness, performing genetic operations to generate a new generation of population, and then judging The termination condition determines whether to iterate again to generate the next generation of the population. Below is the case.
- Comparing the above flow chart, we can simply sort out what the GP system does and wants to do.
- Initialization: Generate a random population after given initial conditions (including terminal sets, function sets, and parameters fitness evaluation by comparing (multiple methods)
- Probabilistic selection based on fitness
- The selected program is used as the parent line, and the next generation is generated by genetic operators such as Crossover, Mutation, and Reproduction.
- Judging whether Termination Criterion is met, if not, continue to iterate
Program Representation
Genetic Programming (GP), is a type of Evolutionary Algorithms. GP inherits the basic idea of Genetic Algorithms. It selects and breeds children from parents. It is different from the traditional coding (fixed-length gene) mode of Genetic Algorithm and the individual of GP is a computer program with diverse performance form. The most common is tree-based genetic programming, which can be expressed in a tree-like structure. In the process of development, GP has naturally expanded a variety of types and expressions, such as linear (Linear GP), graph-based genetic programming (Cartesian GP) and so on.
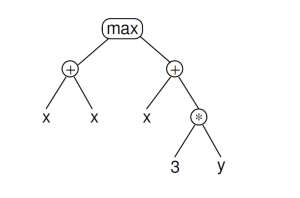
Example: Tree-based representation of the program max(x+x, x+3*y)
The structure of the syntax tree is defined as follows:
The “leaf” part is called the Terminals, which are variables, constants and no-argument functions in the program.
The internal nodes of the tree are called functions, sometimes called primitives, covering functions and operations in the program.
The Primitive set of the GP system is the set of allowed and feasible Functions and Terminals.
In the max(x+x, x+3*y) tree representation above, the terminators are x, y, 3, and the functions are , +, *, max. Then their respective sets are: function set F = {+, *, max}, termination set T = {x, y, 3}
Note: “Function” is not necessarily included in the function set, no-argument functions may be in the termination set
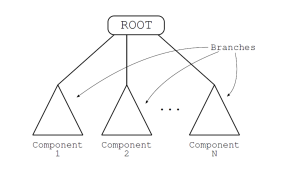
In some GPs the program may be composed of multiple parts, as shown in the figure below, represented by a set of tree branches connected by a special root node.
Fitness and selection
Fitness
Fitness : a value that measures the strengths and weaknesses of an individual, and is a standard for evaluating the quality of an individual’s problem-solving. Analogous to natural species, biological populations with high adaptability to the environment inherit good genes, while those with poor adaptability are naturally eliminated and become extinct.
Fitness function: A function that calculates the fitness of individuals in a population.
Based on different problems, fitness can be measured in various and different ways. Such as the difference between the actual output and the expected output, the resources spent by the system to evolve to the target level, and so on.
The time required for the fitness evaluation process accounts for a large part of the time required for the GP system to run, so the design of the fitness function is generally not recommended to be too complicated.
Selection
Selection refers to the process of selecting individuals based on fitness. The selected individuals will be used as the father line to breed the next generation of program individuals through genetic operators. There are two common selection methods:
Tournament Selection
Tournament selection randomly selects a certain number of individuals from the population, compares their fitness, and the one with the highest fitness is selected as the parent (as the parent) for the next step of genetic operations. Since each time a selection is made, a certain number of individuals (rather than the whole) are randomly selected for comparison, even individuals whose average quality and fitness are not outstanding in the whole group have a chance to be selected, so diversity is achieved.
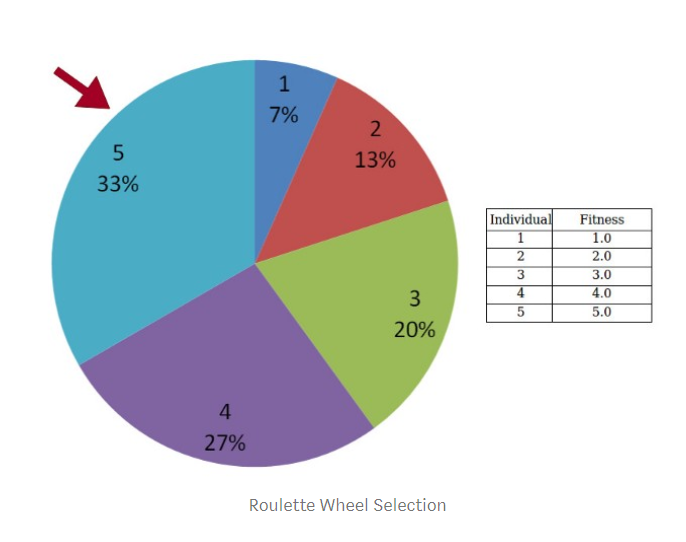
Roulette Wheel Selection
The probability of an individual being selected is proportional to its fitness. Assuming that there is individual 1 in the group, individual 2 … to individual N (the base of the group is N), ⨍ᵢrepresents the fitness of individual i, then the probability that individual i is selected as the parent by the roulette method is ![]() .
.
Illustration: Suppose there are five individuals in the group, and the fitness of individuals with serial numbers 1 to 5 are 1.0, 2.0, 3.0, 4.0, and 5.0, respectively, then the probability of randomly selecting individual 5 is 5.0/(1.0+2.0+3.0+4.0+ 5.0) = 33.33%
Genetic Operators
Crossover
- select a random crossover point in each parent
- copy the tree of one parent as ‘copy_A’
- copy the subtree of the second parent with the crossover point as the root node as ‘subtree_copyB’
- replace the subtree under the Acopy crossover point with Bsubtree_copy, and generate a child.

Mutation
- a mutation point is randomly selected in a parent
- a subtree is randomly generated
- replacing the subtree of the parent with the mutation point as the root node with this randomly generated subtree.

Reproduction (Copy)
Reference
Poli, Riccardo, et al. A Field Guide to Genetic Programming. Lulu Press, 2008. The book may be freely downloaded in electronic form at http://www.gp-field-guide.org.uk.
J. R. Koza. Genetic Programming: On the Programming of Computers by Means of Natural Selection. MIT Press, Cambridge, MA, USA, 1992. ISBN 0-262-11170-5.

 2022/03/24
2022/03/24 2021/09/18
2021/09/18 2019/08/06
2019/08/06 2018/01/18
2018/01/18 2017/12/18
2017/12/18 2017/09/08
2017/09/08